Το μέγεθος και η σύνθεση ενός πληθυσμού μεταβάλλονται μέσα από τις συνεχείς εισόδους και εξόδους ατόμων, οι οποίες με τη σειρά τους καθορίζονται από τις δημογραφικές διεργασίες. Γεννήσεις, θάνατοι, μετακινήσεις εσωτερικές ή εξωτερικές ευθύνονται όχι απλά για το πόσοι άνθρωποι αποτελούν τον πληθυσμό μιας περιοχής αλλά και για τα επί μέρους χαρακτηριστικά του. Η ένταση των δημογραφικών γεγονότων, το ηλικιακό χρονοδιάγραμμα, οι ανά φύλο, επίπεδο εκπαίδευσης ή βαθμό αστικότητας διαφοροποιήσεις της επίδρασης των δημογραφικών γεγονότων διαμορφώνουν τη δομή και σύνθεση ενός πληθυσμού. Και αντίθετα, η δομή και σύνθεση ενός πληθυσμού επηρεάζουν τη συχνότητα εμφάνισης συγκεκριμένων δημογραφικών γεγονότων.

Δύο πληθυσμοί με παραπλήσιους αδρούς δείκτες θνησιμότητας αλλά με διαφορετική κατά ηλικία θνησιμότητα δεν έχουν την ίδια ηλικιακή δομή ούτε την ίδια δυναμική. Παράλληλα οι δημογραφικές διεργασίες παρουσιάζουν σημαντικές γεωγραφικές και διαχρονικές διαφοροποιήσεις ως προς την ένταση και το χρονοδιάγραμμα. Η μελέτη των γεωγραφικών διαφοροποιήσεων και η κατανόηση των διαχρονικών εξελίξεων αποτελούν σημαντικό κομμάτι της δημογραφικής ανάλυσης.

Από την ίδια τη φύση του αντικειμένου της, η Δημογραφία προσφέρεται για την ανάπτυξη και χρήση μοντέλων. Η δημογραφική ανάλυση μέσα από την εμπειρική μελέτη του πληθυσμού και συγκεκριμένων υπο-ομάδων του αναζητά «κανονικότητες» στο χρονοδιάγραμμα γεγονότων όπως γάμος, γέννηση παιδιού, μετανάστευση ή θάνατος που συμβαίνουν στον κύκλο ζωής ενός ατόμου. Αποτέλεσμα μιας τέτοιας άσκησης αποτελούν, για παράδειγμα, οι πίνακες επιβίωσης. Ο σκοπός της δημογραφικής ανάλυσης δεν ολοκληρώνεται με την αποτύπωση τέτοιων μοντέλων ή τον εντοπισμό κάποιων σημαντικών διαφοροποιήσεων ή ομοιοτήτων. Αντίθετα η αξία τους αποτιμάται ανάλογα με την περαιτέρω χρησιμότητά τους σε αναλύσεις και έρευνες πέρα του στενού δημογραφικού ενδιαφέροντος.

Στις ενότητες που ακολουθούν παρουσιάζονται κάποιες μέθοδοι και τεχνικές που χρησιμοποιούνται στη δημογραφική ανάλυση, όπως η τυποποίηση ως προς την ηλικία, η κατασκευή πινάκων επιβίωσης, οι πληθυσμιακές προβολές και παρουσιάζεται το μοντέλο του σταθερού πληθυσμού.

 

5.1. Τυποποίηση ως προς την ηλικία (Age-standardization)

Από όλα τα δημογραφικά χαρακτηριστικά, η ηλικία αποτελεί το σημαντικότερο παράγοντα που επηρεάζει τη συχνότητα εμφάνισης κάθε δημογραφικού γεγονότος. Η πιθανότητα απόκτησης ενός (επιπλέον) παιδιού, η πιθανότητα μετακίνησης και η πιθανότητα θανάτου καταγράφουν σημαντικές διαφοροποιήσεις σε σχέση με την ηλικία. Επιπλέον, η ηλικιακή δομή ενός πληθυσμού μεταβάλλεται διαρκώς υπό την ασύμμετρη επίδραση των διαφορετικών δημογραφικών φαινομένων. Ο αριθμός των ατόμων που αποτελούν τη βάση της ηλικιακής πυραμίδας καθορίζεται κυρίως από τις γεννήσεις, ενώ η κορυφή της πυραμίδας διαμορφώνεται κυρίως από τη θνησιμότητα. Κατά συνέπεια, κατά τη διαχρονική μελέτη της δημογραφικής συμπεριφοράς ενός πληθυσμού ή κατά τη σύγκριση διαφορετικών πληθυσμών πρέπει να λαμβάνονται υπ’ όψιν οι ενδεχόμενες διαφορο-ποιήσεις στην ποσοστιαία κατανομή των ατόμων ανά ηλικιακή ομάδα.

Αυτό επιτυγχάνεται με την τυποποίηση των δεικτών ως προς την ηλικία (age standardization). Στόχος της τυποποίησης είναι η εφαρμογή των ειδικών κατά ηλικία δεικτών διαφορετικών πληθυσμών σε έναν «πρότυπο» πληθυσμό (standard population) συγκεκριμένης ηλικιακής κατανομής (Preston et al. 2001). Με τον τρόπο αυτό οι νέοι τυποποιημένοι ως προς την ηλικία δείκτες είναι απαλλαγμένοι από την επίδραση της διαφορετικής ηλικιακής δομής στη διαμόρφωσή τους και κατά συνέπεια είναι απολύτως συγκρίσιμοι.

Η τυποποίηση γίνεται με δύο διαφορετικές μεθόδους, ανάλογα με την ηλικιακή κατανομή που επιλέγεται ως πρότυπο.

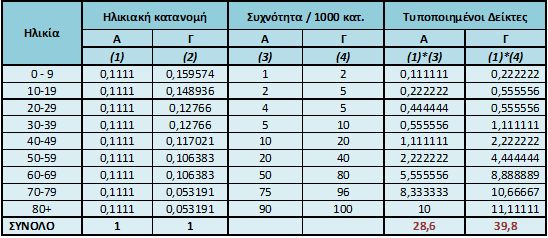
Στην πρώτη μέθοδο επιλέγεται ένας από τους συγκρινόμενους πληθυσμούς ως «πρότυπο» πάνω στον οποίο εφαρμόζονται οι ειδικοί κατά ηλικία δείκτες των άλλων πληθυσμών (Πίνακας 5.2).

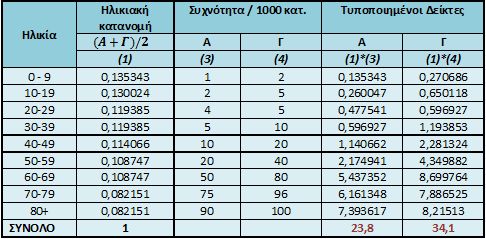
Στη δεύτερη μέθοδο ως «πρότυπο» επιλέγεται μια ανεξάρτητη ηλικιακή κατανομή πάνω στην οποία εφαρμόζονται οι διαφορετικοί κατά ηλικία συντελεστές (Πίνακας 5.3).

Εφαρμογή: Ο παρακάτω πίνακας συνοψίζει τις πληροφορίες σχετικά με τους υποθετικούς πληθυσμούς Α, Β, Γ της ενότητας §4.2.

Πίνακας 5.1 Παράδειγμα υποθετικών πληθυσμών.

 

Οι πληθυσμοί Α και Γ καταγράφουν τον ίδιο αριθμό θανάτων ανά 1000 κατοίκους, αν και οι ειδικοί κατά ηλικία δείκτες είναι πολύ διαφορετικοί. Το ερώτημα που προκύπτει είναι το ακόλουθο: Αν οι πληθυσμοί είχαν την ίδια ηλικιακή κατανομή πώς θα διαμορφώνονταν οι δείκτες; Απάντηση στο παραπάνω ερώτημα δίνει η τεχνική της τυποποίησης ως προς την ηλικία.

1η μέθοδος τυποποίησης: Υπολογισμός των τυποποιημένων δεικτών ως προς την ηλικιακή κατανομή του πληθυσμού Α. Σε αυτήν την ηλικιακή κατανομή εφαρμόζεται η ειδική κατά ηλικία θνησιμότητα, όπως:

 

Πίνακας 5.2 1η μέθοδος τυποποίησης.

 

Μετά την τυποποίηση ως προς την ηλικία, προκύπτει ότι η ένταση του φαινομένου είναι σημαντικά μεγαλύτερη στον πληθυσμό Γ σε σχέση με τον πληθυσμό Α (39,8 έναντι 28,6 συμβάντων ανά 1.000 κατ.).

Ανάλογα θα μπορούσε να χρησιμοποιηθεί η ηλικιακή κατανομή του πληθυσμού Γ ως πρότυπο υπολογισμού του τυποποιημένου δείκτη. Στην περίπτωση αυτή, οι τυποποιημένοι δείκτες των πληθυσμών Α και Γ θα ήταν 19,0 και 28,6 συμβάντα ανά 1000 κατ., αποδίδοντας και πάλι αρκετά χαμηλότερη τιμή στον πληθυσμό Α σε σχέση με τον Γ.

2η μέθοδος τυποποίησης: Εναλλακτικά θα μπορούσε να χρησιμοποιηθεί μια τρίτη ηλικιακή κατανομή ως πρότυπο. Αυτή θα μπορούσε να ήταν η ηλικιακή κατανομή ενός πραγματικού ή υποθετικού πληθυσμού, ή ακόμη η μέση ηλικιακή κατανομή των εξεταζόμενων πληθυσμών, όπως φαίνεται στον παρακάτω πίνακα.

Πίνακας 5.3 2η μέθοδος τυποποίησης.

 

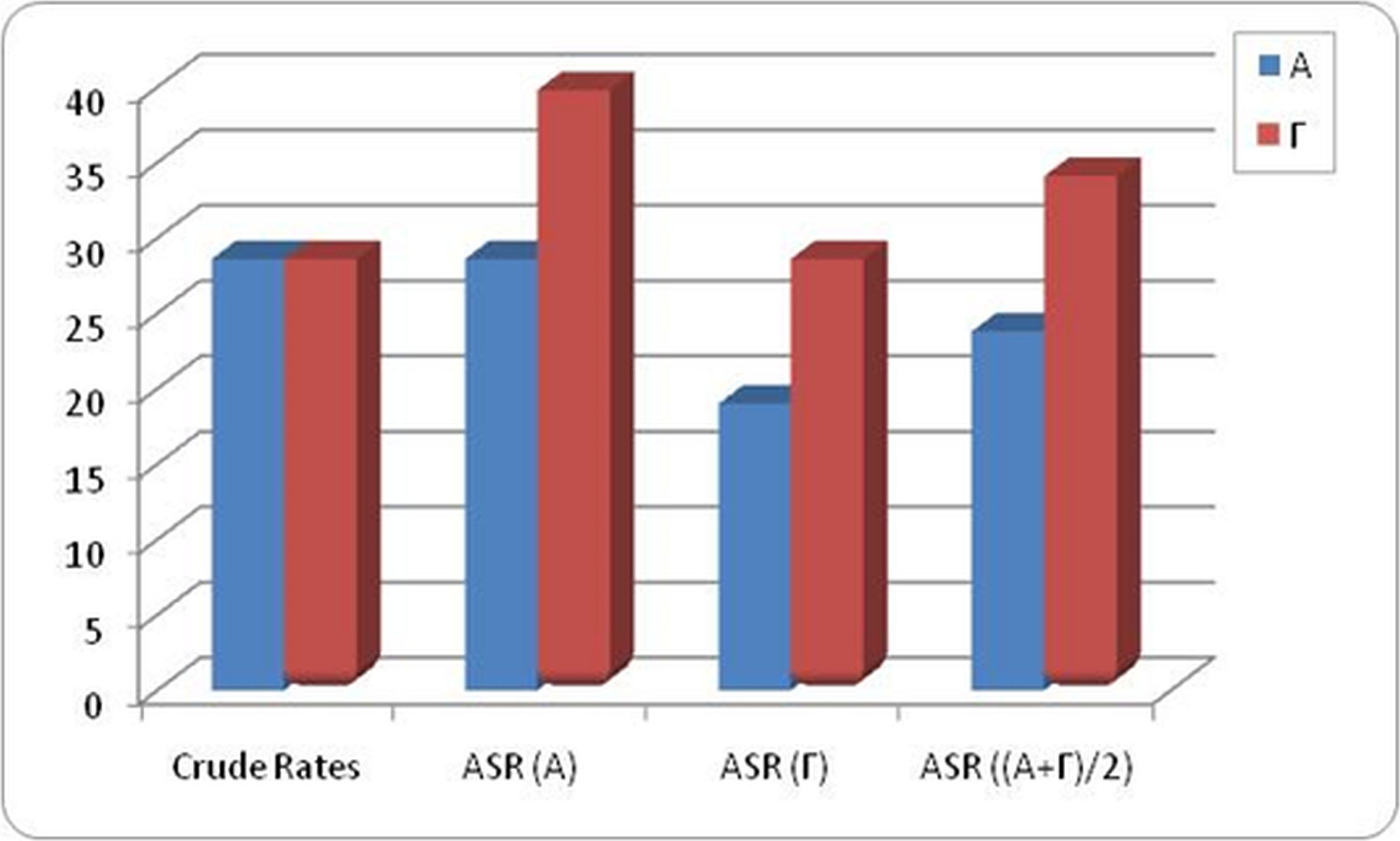
Οι παραπάνω δείκτες είναι υποθετικοί και θα προέκυπταν αν οι πληθυσμοί Α και Γ είχαν την ίδια ηλικιακή κατανομή. Είναι σημαντικό να τονιστεί πως οι τυποποιημένοι δείκτες είναι τεχνητοί δείκτες αφού προκύπτουν από μια υποθετική ηλικιακή κατανομή και εξαρτώνται από αυτήν. Όπως προκύπτει από τους παραπάνω υπολογισμούς, ανάλογα με το πρότυπο τυποποίησης προκύπτουν διαφορετικοί τυποποιημένοι κατά ηλικία δείκτες, η διαφορά όμως μεταξύ των συγκρινόμενων πληθυσμών παραμένει σχεδόν σταθερή (Διάγραμμα 5.1).

Σημείωση: ASR(A), ASR(Γ) και ASR((A+Γ)/2) αντιστοιχούν στους δείκτες που έχουν τυποποιηθεί ως προς την ηλικιακή κατανομή του πληθυσμού Α, Γ και του μέσου όρου αντίστοιχα.

Διάγραμμα 5.1 Σύγκριση Αδρών και Τυποποιημένων Δεικτών δύο πληθυσμών -με διαφορετικές μεθόδους τυποποίησης.

 

Το σημαντικό αποτέλεσμα από την παραπάνω άσκηση είναι ότι ανεξάρτητα της μεθόδου τυποποίησης ο πληθυσμός Α έχει σταθερά χαμηλότερο τυποποιημένο δείκτη σε σχέση με τον πληθυσμό Γ. Το γεγονός ότι αυτή η διαφορά «χάνεται» κατά τον υπολογισμό των αδρών δεικτών φανερώνει τη σημαντική επίδραση της ηλικιακής δομής στη διαμόρφωση των συγκεκριμένων δεικτών και αναδεικνύει την αναγκαιότητα τυποποίησης του δείκτη ως προς αυτήν.

Κατά απόλυτη αναλογία, η τυποποίηση ως προς την ηλικιακή δομή είναι απαραίτητη όταν μελετάται η διαχρονική εξέλιξη ενός δείκτη. Δεδομένου ότι, κατά κανόνα, η κατά ηλικία κατανομή του πληθυσμού δεν είναι σταθερή στο πέρασμα του χρόνου, μεταβολές στους αδρούς δείκτες δεν αποτυπώνουν την πραγματική μεταβολή της δημογραφικής συμπεριφοράς ενός πληθυσμού.

 

5.2. Πίνακες Επιβίωσης (Life Tables)

Πίνακας επιβίωσης καλείται ο πίνακας που αποτυπώνει την κατά ηλικία πιθανότητα θανάτου που διατρέχουν τα άτομα ενός πληθυσμού, μια συγκεκριμένη χρονική στιγμή. Πρόκειται για μια από τις χρήσιμες δημογραφικές επινοήσεις που βρίσκει εφαρμογή σε διάφορα άλλα επιστημονικά πεδία. Αν και φαινομενικά πρόκειται για μια απλή και συνολική απεικόνιση της θνησιμότητας ενός πληθυσμού και των ηλικιακών της διακυμάνσεων, στην πραγματικότητα σε έναν πίνακα επιβίωσης αποτυπώνονται διαφορετικοί σύνθετοι δείκτες που παρέχουν πληροφορίες για τη δυναμική του πληθυσμού. Πέρα από τους ειδικούς κατά ηλικία δείκτες θνησιμότητας, στους πίνακες επιβίωσης μπορεί κανείς να «διαβάσει» πληροφορίες για τους κατά ηλικία δείκτες επιβίωσης (survival rates), το προσδόκιμο ζωής κατά τη γέννηση (life expectancy at birth), τα εναπομείναντα έτη ζωής σε διαφορετικές ηλικίες (remaining life expectancy at different ages), το ποσοστό των επιζώντων ανά έτος γέννησης κ.α..

Όπως ήδη αναφέρθηκε στο Κεφάλαιο 1, οι πρώτοι πίνακες επιβίωσης καταρτίστηκαν σχεδόν από τα πρώτα στάδια της δημογραφικής μελέτης, στα μέσα του 17ου αιώνα, βάσει της συστηματικής δουλειάς των John Graunt και Edmund Halley. Σήμερα μέσα από συνεχείς βελτιώσεις και αναβαθμίσεις οι πίνακες επιβίωσης χαίρουν ευρείας θεωρητικής και πρακτικής εφαρμογής.

Το μόνο που απαιτείται για την κατασκευή ενός πίνακα επιβίωσης είναι η κατά ηλικία κατανομή του πληθυσμού και των θανάτων που συμβαίνουν σε αυτόν. Δεδομένου του διαφορετικού κινδύνου που τα δύο φύλα αντιμετωπίζουν απέναντι στο θάνατο, καταρτίζονται χωριστοί πίνακες επιβίωσης για άνδρες και γυναίκες.

Υπάρχουν διαφορετικοί τύποι πινάκων επιβίωσης, ανάλογα με τα δεδομένα που χρησιμοποιούνται στον υπολογισμό των δεικτών. Αν οι δείκτες θνησιμότητας αποτυπώνουν τη συμπεριφορά μιας γενιάς προκύπτουν οι πίνακες επιβίωσης γενιάς ενώ αν αναφέρονται σε μια χρονική περίοδο προκύπτουν πίνακες περιόδου. Οι πίνακες επιβίωσης γενιάς (cohort life tables) αποτυπώνουν την πραγματική πιθανότητα θανάτου που αντιμετωπίζουν σε κάθε ηλικία τα άτομα με κοινό έτος γέννησης. Οι πίνακες γενιάς αναφέρονται στη θνησιμότητα όπως βιώνεται από πραγματικές γενιές. Για να καταρτιστεί ένας πίνακας γενιάς πρέπει να παρακολουθηθούν τα άτομα μιας συγκεκριμένης γενιάς σε όλη τη διάρκεια της ζωής προκειμένου να υπολογισθεί η πιθανότητα θανάτου σε κάθε ηλικία. Για παράδειγμα ο πίνακας επιβίωσης της γενιάς του 1950 δεν μπορεί να ολοκληρωθεί πριν αποβιώσει και το τελευταίο άτομο που ανήκει σε αυτή την γενιά, δηλαδή όχι πριν το 2050 ή ίσως και ακόμη αργότερα. Για το λόγο αυτό οι πίνακες επιβίωσης συνήθως αναφέρονται σε μια περίοδο. Στους πίνακες επιβίωσης περιόδου (period life tables) χρησιμοποιούνται οι κατά ηλικία δείκτες θνησιμότητας μιας συγκεκριμένης χρονικής περιόδου (συνήθως ενός έτους) θεωρώντας ότι είναι η θνησιμότητα που υφίστανται στις διάφορες ηλικίες τα άτομα μιας υποθετικής γενιάς (10.000 ή 100.000 ατόμων) κατά τη διάρκεια της ζωής τους.

Οι πίνακες επιβίωσης μπορεί να είναι πλήρεις (unabridged) αν χρησιμοποιούνται μονοετείς ηλικιακές ομάδες ή συνεπτυγμένοι (abridged) αν χρησιμοποιούνται 5-ετείς ηλικιακές ομάδες. Οι πλήρεις πίνακες είναι αναλυτικότεροι και αποτυπώνουν με μεγαλύτερη λεπτομέρεια και ακρίβεια την επιτυχία με την οποία αντιμετωπίζει ένας πληθυσμός το θάνατο. Οι πλήρεις πίνακες χρησιμοποιούνται σε αναλύσεις βιοστατιστικής ή αναλογιστικής, όπου η ακρίβεια και η λεπτομέρεια είναι απολύτως αναγκαίες. Οι συνεπτυγμένοι πίνακες απαιτούν μικρότερο όγκο δεδομένων για να καταρτιστούν και είναι συχνά βολικότεροι στην ανάλυση.

5.2.1. Κατασκευή Πινάκων Επιβίωσης

Σ’ έναν κλασικό πίνακα επιβίωσης, η πρώτη στήλη αναφέρεται πάντα στην ηλικία x. Στην περίπτωση την οποία οι πίνακες είναι πλήρεις εκφράζεται σε μονοετείς ομάδες ηλικιών δηλαδή x= 0,1,2,3,.....w (όπου συνήθως w=100).

Στην περίπτωση των συμπτυγμένων πινάκων η ηλικία εκφράζεται ως διάστημα της μορφής (x, x+n) όπου συνήθως n=5 ή 10,

δηλαδή x= 0,1,5,10,15,. n=5
ή x= 0,1,5,10,20,... n=10

Δεν είναι απαραίτητο σ’ έναν πίνακα επιβίωσης το εύρος n των διαστημάτων των ηλικιών να παραμένει σταθερό σε όλες τις ηλικιακές ομάδες. Σε κάθε περίπτωση, το πρώτο έτος ζωής εξετάζεται χωριστά, ενώ η δεύτερη ηλικιακή ομάδα είναι συνήθως 4-ετής και αφορά τις ηλικίες από ενός έως πέντε ετών [1,5). Αυτό επιβάλλεται λόγω της σημαντικά υψηλότερης θνησιμότητας κατά τη βρεφική και πρώτη παιδική ηλικία.

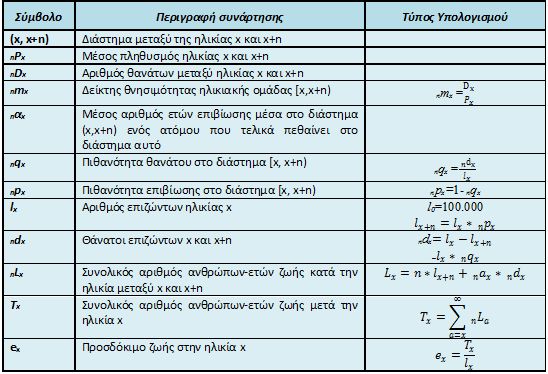
Η κάθε μια από τις υπόλοιπες στήλες του πίνακα παρουσιάζει μια παράμετρο της θνησιμότητας ή επιβίωσης, εκφρασμένη ως συνάρτηση της ηλικίας x (Preston et al. 2001). Οι συμβολισμοί, η περιγραφή και ο τρόπος υπολογισμού αυτών των συναρτήσεων παρουσιάζονται στον Πίνακα 5.4.

Απ’ όλες τις στήλες, αυτή που χρησιμοποιείται και αναλύεται περισσότερο είναι η τελευταία στήλη η οποία απεικονίζει το προσδόκιμο ζωής κατά τη γέννηση e0, καθώς για κάθε ηλικία ex, που περιγράφει το μέσο αριθμό επιπλέον ετών ζωής τον οποίο προσδοκάται να έχει ένα άτομο που έχει επιζήσει μέχρι την ηλικία x. Έχει ενδιαφέρον να σημειωθεί ότι συχνά το e1 > e0, γεγονός που αποδίδεται στην υψηλή θνησιμότητα κατά το πρώτο έτος ζωής. Επιβιώνοντας του κρίσιμου πρώτου έτους, ένα παιδί μπορεί να προσδοκά ότι θα ζήσει περισσότερο από ένα νεογέννητο.

Πίνακας 5.4 Περιγραφή μεταβλητών και συναρτήσεων ενός Πίνακα Επιβίωσης.

 

Κάποιες από τις παραπάνω συναρτήσεις παρουσιάζονται αναλυτικότερα για την καλύτερη κατανόησή τους:

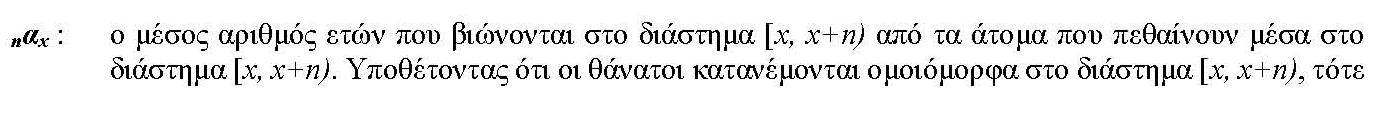
Πίνακας 5.5 Η Δομή του Πίνακα Επιβίωσης.

 

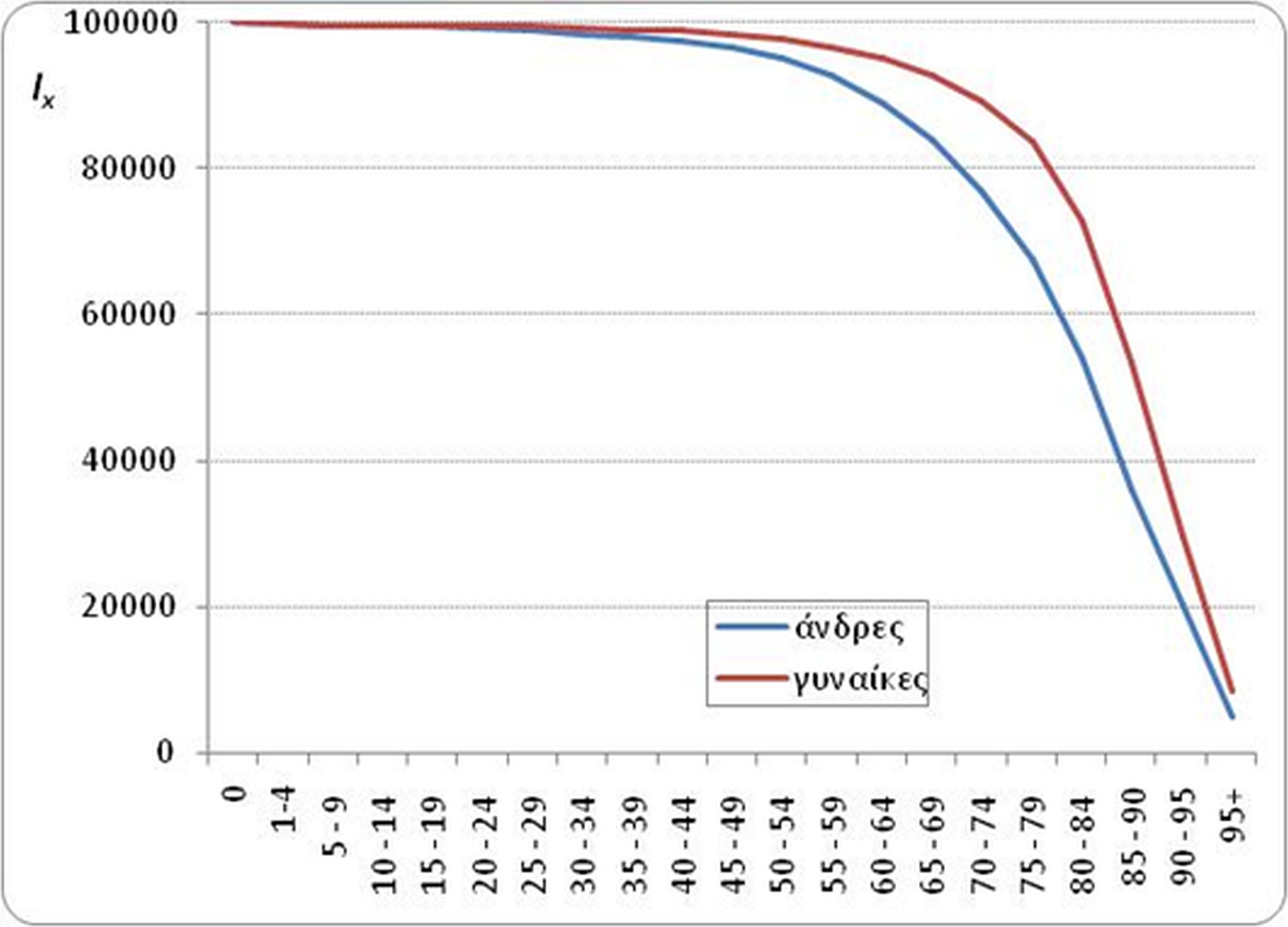
Πίνακας 5.6 Πίνακας Επιβίωσης Αρρένων, Ελλάδα 2012.

 

5.2.2. Ερμηνεία ενός Πίνακα Επιβίωσης

Όπως έχει ήδη αναφερθεί ένας πίνακας επιβίωσης δίνει πολλές και ενδιαφέρουσες πληροφορίες σχετικά με τη θνησιμότητα και τη δυναμική ενός πληθυσμού (Preston et al. 2001).

Κάποια βασικά στοιχεία δίνονται απευθείας, διαβάζοντας τις στήλες του πίνακα (Πίνακας 5.5). Συγκεκριμένα, και χρησιμοποιώντας τα στοιχεία του παραπάνω πίνακα (Πίνακας 5.6) προκύπτουν οι παρακάτω πληροφορίες σχετικά με τον ανδρικό πληθυσμό της Ελλάδας το 2012:

Χρησιμοποιώντας τα στοιχεία του Πίνακα 5.6 προκύπτουν οι ακόλουθες συμπληρωματικές πληροφορίες σχετικά με την πιθανότητα επιβίωσης του ανδρικού πληθυσμού της Ελλάδας το 2012:

Η πιθανότητα επιβίωσης, η πιθανότητα θανάτου καθώς και ο αριθμός των επιζώντων σε κάθε ηλικιακή ομάδα παριστάνονται γραφικά με τη βοήθεια των παρακάτω διαγραμμάτων.

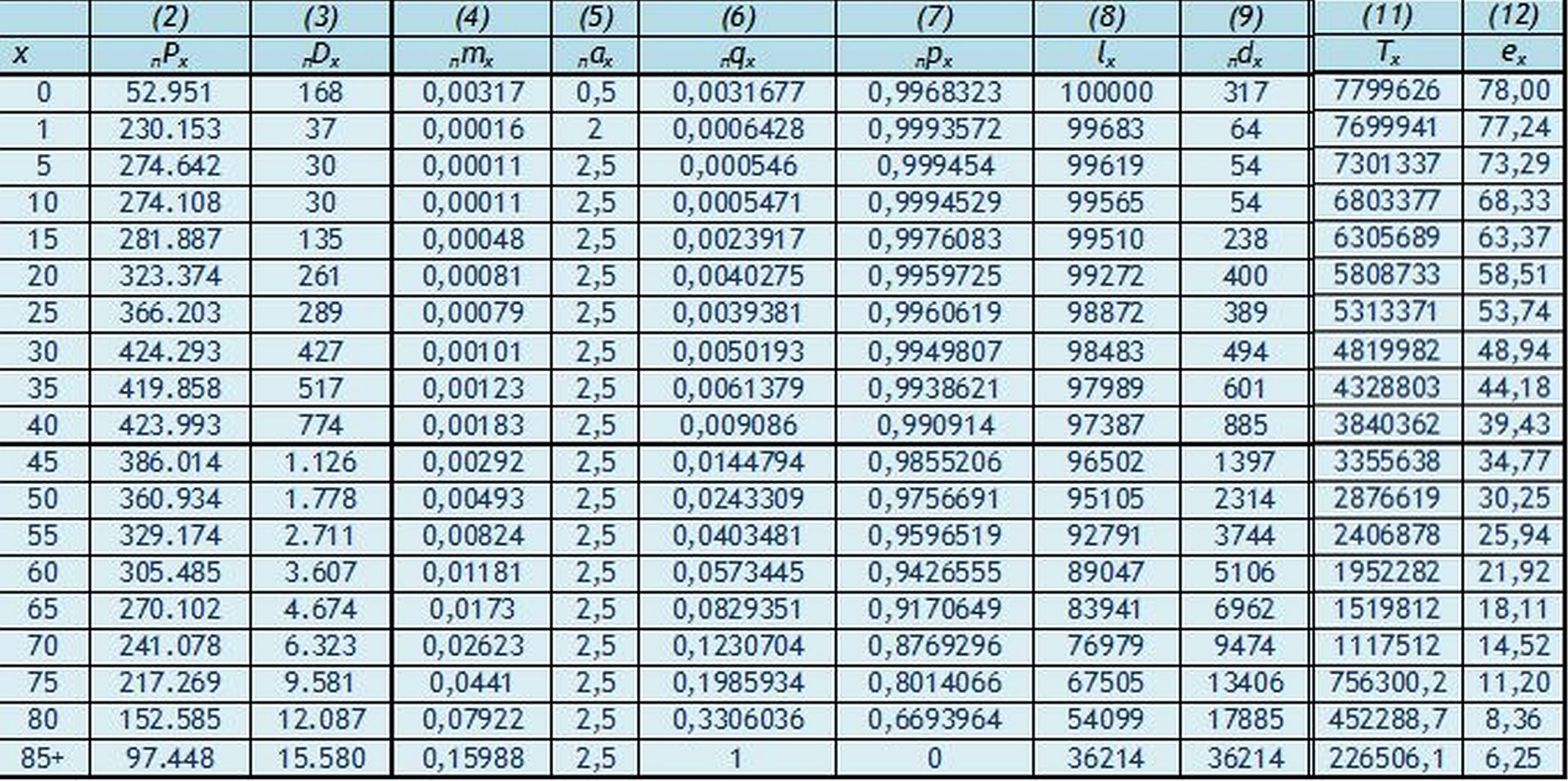
Μια από τις πρώτες και πιο ενδιαφέρουσες διαπιστώσεις αφορά στο σχετικά αμετάβλητο μεταξύ διαφορετικών πληθυσμών, μοτίβο της πιθανότητας θανάτου ανά ηλικία. Παρά τις διαφοροποιήσεις, ως προς την ένταση της θνησιμότητας, η καμπύλη της πιθανότητας θανάτου παραμένει διαχρονικά και γεωγραφικά σταθερή (Διάγραμμα 5.2).

Οι ειδικοί κατά ηλικία δείκτες θνησιμότητας είναι σχετικά υψηλοί το πρώτο έτος ζωής του ατόμου (Διάγραμμα 5.2). 

Σημείωση: Η χρήση λογαριθμικής κλίμακας επιτρέπει τη λεπτομερέστερη παρουσίαση των διαφοροποιήσεων στις νεαρές ηλικίες.

Διάγραμμα 5.2 Ειδικοί κατά ηλικία δείκτες θνησιμότητας (_nm_x), Άνδρες και Γυναίκες, Ελλάδα 2012.

 

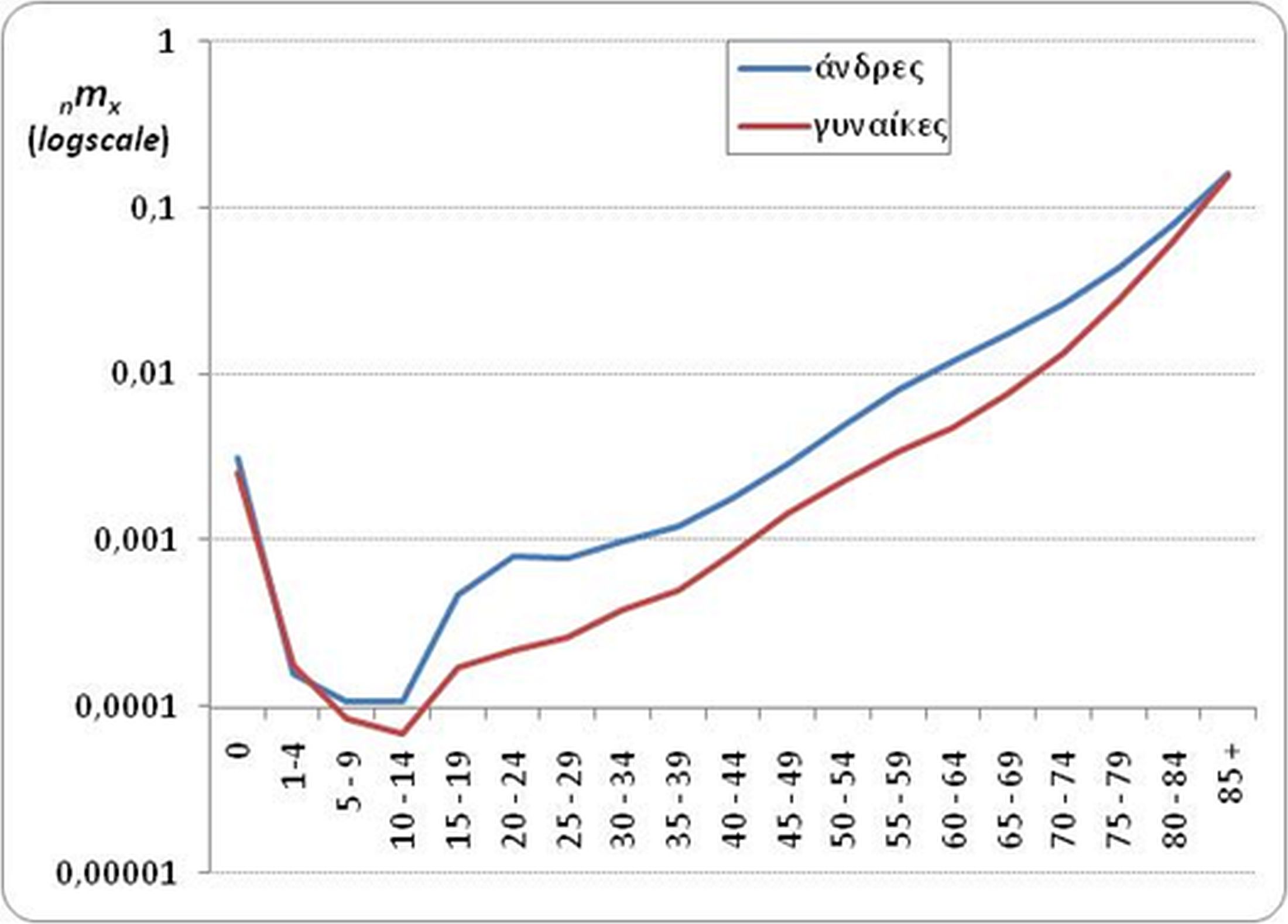
Μετά το πρώτο και μέχρι το τέταρτο έτος ζωής η πιθανότητα θανάτου μειώνεται συστηματικά και είναι σχεδόν μηδενική μέχρι το 14ο έτος ζωής. Από το 15ο έτος και μετά, η πιθανότητα θανάτου σταδιακά αυξάνεται με την ηλικία. Σε όλες τις ηλικίες η πιθανότητα θανάτου των ανδρών είναι σταθερά υψηλότερη εκείνης των γυναικών (Διάγραμμα 5.3).

Διάγραμμα 5.3 Πιθανότητα θανάτου κατά ηλικία (_nq_x), Ανδρες και Γυναίκες, Ελλάδα 2012.

 

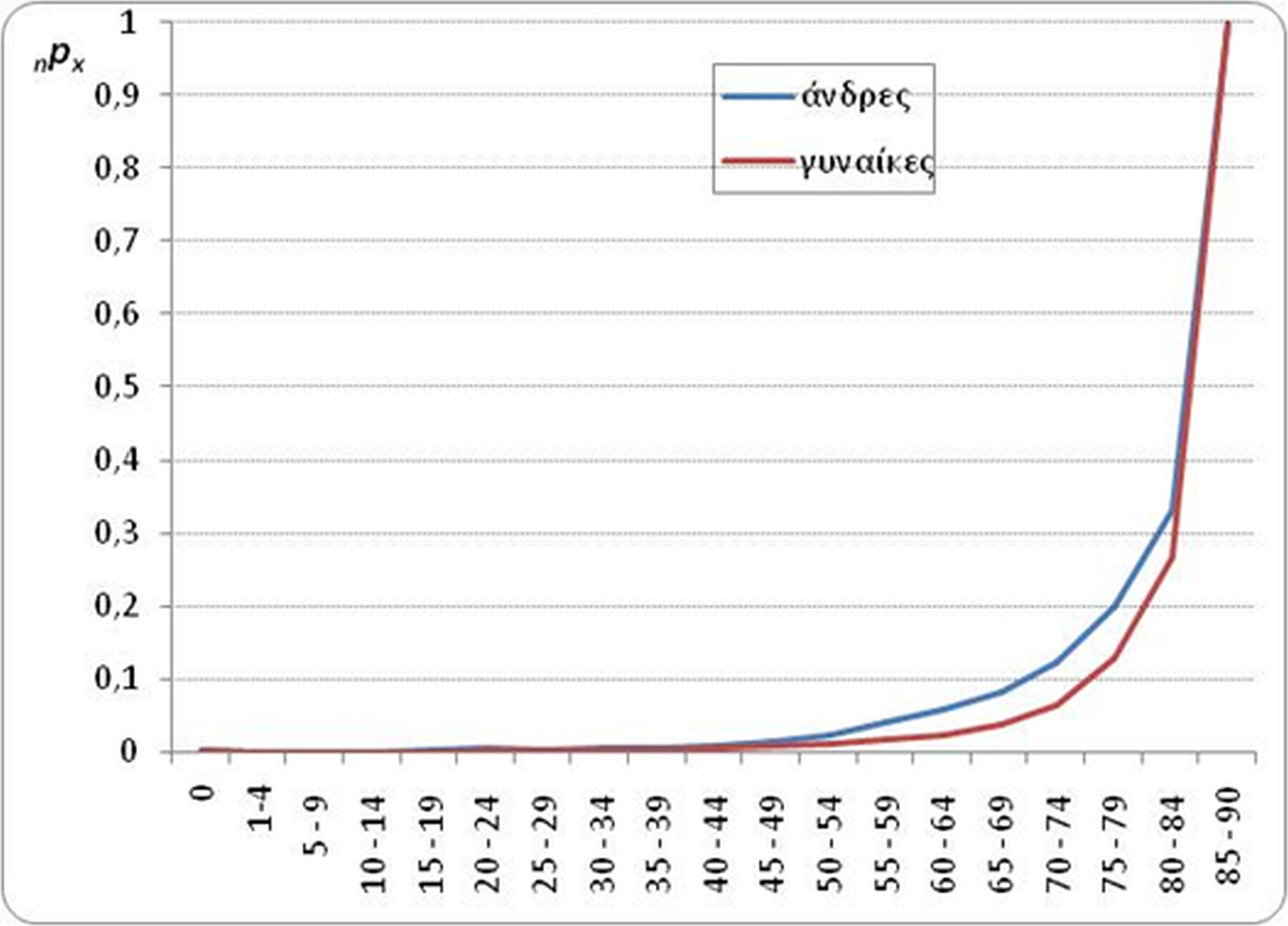
Ανάλογα αποτυπώνονται οι επιζώντες κάθε ηλικιακής ομάδας (Διάγραμμα 5.4).

 

Διάγραμμα 5.4 Επιζώντες κατά ηλικία (l_x),Άνδρες και Γυναίκες, Ελλάδα 2012.

 

Σε περιπτώσεις πληθυσμών όπου τα απαραίτητα στατιστικά στοιχεία για την κατάρτιση πινάκων επιβίωσης δεν είναι διαθέσιμα, οι δείκτες επιβίωσης μπορούν να υπολογισθούν από πρότυπους πίνακες επιβίωσης. Ένας πρότυπος πίνακας επιβίωσης (model life table) προκύπτει από τις στατιστικές θανάτου διαφορετικών πληθυσμών (ή χωρών) με κοινά μεταξύ τους χαρακτηριστικά (Preston aet al. 2001). Στόχος των πρότυπων πινάκων είναι η χρήση τους σε χώρες οι οποίες δεν διαθέτουν πλήρη ή αξιόπιστα στοιχεία ως προς τη φυσική κίνηση του πληθυσμού. Το 1955, τα Ηνωμένα Έθνη, χρησιμοποιώντας τη μέθοδο ανάλυσης παλινδρόμησης δημοσίευσαν τους πρώτους πρότυπους πίνακες επιβίωσης. Το 1966, οι Coale and Denemy εισήγαγαν του περιφερειακούς πρότυπους πίνακες. Μελετώντας τους πίνακες επιβίωσης 326 πληθυσμών κατάφεραν να αναπτύξουν 200 διαφορετικούς πρότυπους πίνακες. Η επιλογή του κατάλληλου για κάθε περίπτωση προτύπου γίνεται βάσει μιας σειράς γεωγραφικών και δημογραφικών κριτηρίων, όπως είναι το επίπεδο βρεφικής και παιδικής θνησιμότητας, οι διαφορές μεταξύ φύλων κλπ..

 

 5.3. Σταθερός πληθυσμός (Stable population model)

Το υπόδειγμα του σταθερού πληθυσμού χρησιμοποιείται ευρύτατα στη δημογραφική ανάλυση για την περιγραφή και κατανόηση της δομής, ανάπτυξης και εξέλιξης των πληθυσμών (Weinstein and Pillai, 2001). Σταθερός καλείται ο κλειστός πληθυσμός του οποίου οι ειδικοί κατά ηλικία δείκτες γονιμότητας και θνησιμότητας παραμένουν διαχρονικά αμετάβλητοι. Αποδεικνύεται μαθηματικά ότι πληθυσμοί με σταθερούς κατά ηλικία δείκτες γονιμότητας και θνησιμότητας αυξάνονται (ή μειώνονται) με σταθερό ρυθμό και αποκτούν μια χαρακτηριστική και επίσης διαχρονικά αμετάβλητη ηλικιακή δομή.

Μια ειδική περίπτωση σταθερού πληθυσμού είναι ο στάσιμος πληθυσμός. Στάσιμος καλείται ένας σταθερός πληθυσμός με μηδενικό ρυθμό αύξησης (zero population growth rate), ο οποίος ούτε αυξάνεται ούτε μειώνεται διαχρονικά. Ένας στάσιμος πληθυσμός πέρα από τη σταθερή ηλικιακή δομή έχει και σταθερό μέγεθος.

Αν και από τα μέσα του 20ου αιώνα ελάχιστοι είναι πλέον οι πληθυσμοί που καταγράφουν σταθερά επίπεδα γονιμότητας και θνησιμότητας και επομένως προσεγγίζονται από το μοντέλο του σταθερού πληθυσμού, η χρησιμότητα του μοντέλου στη δημογραφική ανάλυση παραμένει ιδιαίτερα σημαντική. Πρώτον, συμβάλλει σημαντικά στη θεωρητική αναζήτηση της σχέσης και της αλληλεπίδρασης μεταξύ γονιμότητας, θνησιμότητας, πληθυσμιακής δομής και ανάπτυξης. Δεύτερον, χρησιμοποιείται για την κάλυψη κενών στα εμπειρικά δεδομένα, σε περιπτώσεις όπου τα τελευταία είναι είτε μη διαθέσιμα είτε αναξιόπιστα. Τρίτον, κατανοώντας τις ιδιότητες ενός σταθερού πληθυσμού γίνονται καλύτερα αντιληπτές οι συνέπειες της ραγδαίας μείωσης γονιμότητας και θνησιμότητας που καταγράφεται σε όλον τον κόσμο μέσα στον 210 αιώνα. Τέλος, χρησιμοποιώντας ως βάση το μοντέλο του σταθερού πληθυσμού, διατυπώθηκαν και αναπτύχθηκαν έννοιες όπως το “population momentum”.

5.3.1. Ιδιότητες σταθερού πληθυσμού

Διατηρώντας διαχρονικά αμετάβλητες τις συνθήκες θνησιμότητας και γονιμότητας και μηδενική τη μετανάστευση, ένας πληθυσμός αποκτά σταθερό (θετικό ή αρνητικό) ρυθμό αύξησης (r) και διατηρεί σταθερή την ηλικιακή δομή του. Σταθερή ηλικιακή δομή σημαίνει ότι η ποσοστιαία αναλογία της κάθε ηλικιακής ομάδας δε μεταβάλλεται. Ωστόσο, ο συνολικός πληθυσμός, καθώς κι ο αριθμός των ατόμων κάθε ηλικιακής ομάδας μπορεί να αυξάνεται (αν r>0) ή να μειώνεται (αν r<0), με κοινό όμως ρυθμό ώστε η συμμετοχή της κάθε ηλικιακής ομάδας στο συνολικό πληθυσμό να παραμένει σταθερή.

Στην ειδική περίπτωση του στάσιμου πληθυσμού, όπου r=0, αμετάβλητα στο χρόνο παραμένουν τόσο η αναλογία κάθε ηλικιακής ομάδας όσο και το απόλυτο μέγεθος κάθε μιας από αυτές.

Ένας σταθερός πληθυσμός έχει εκθετικό ρυθμό αύξησης.

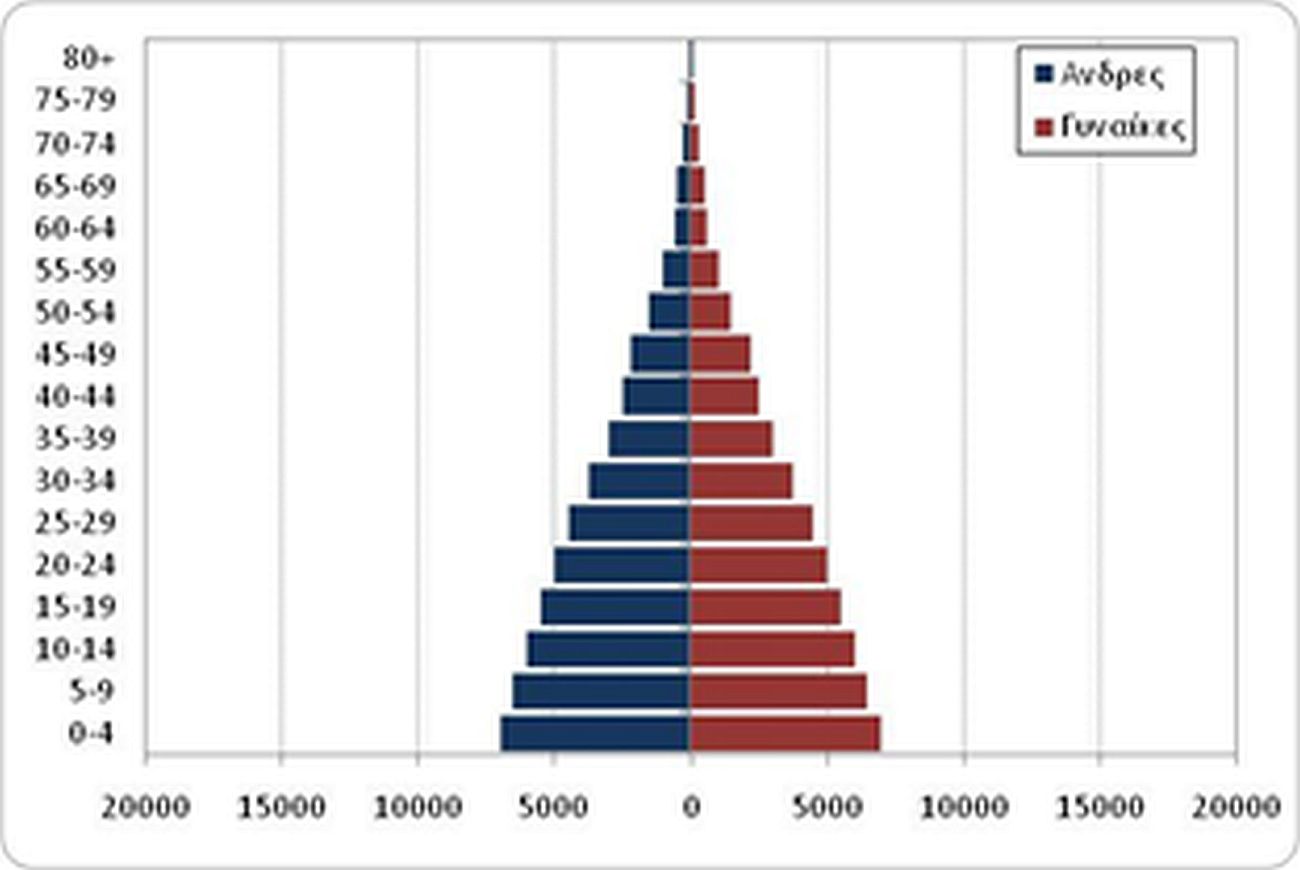
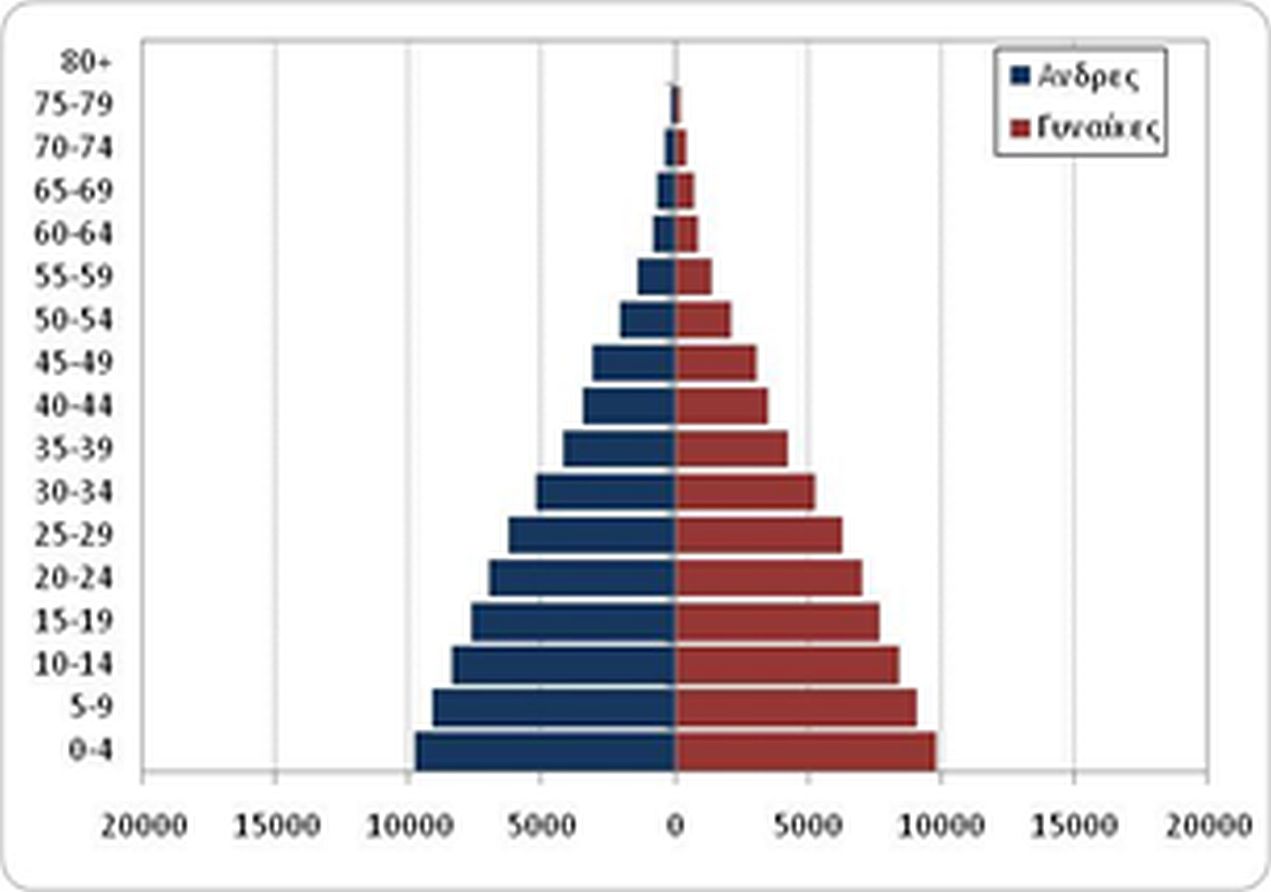
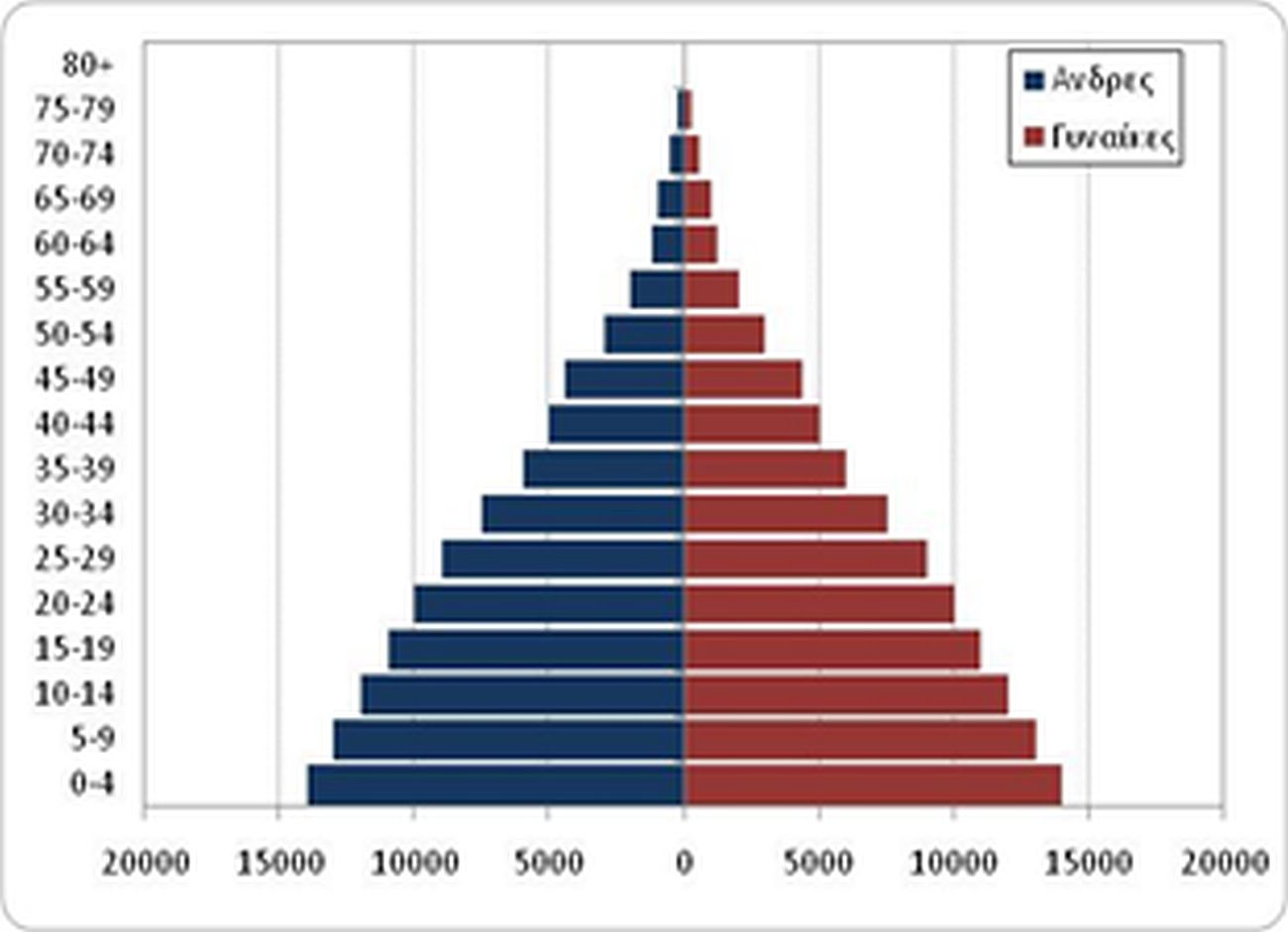
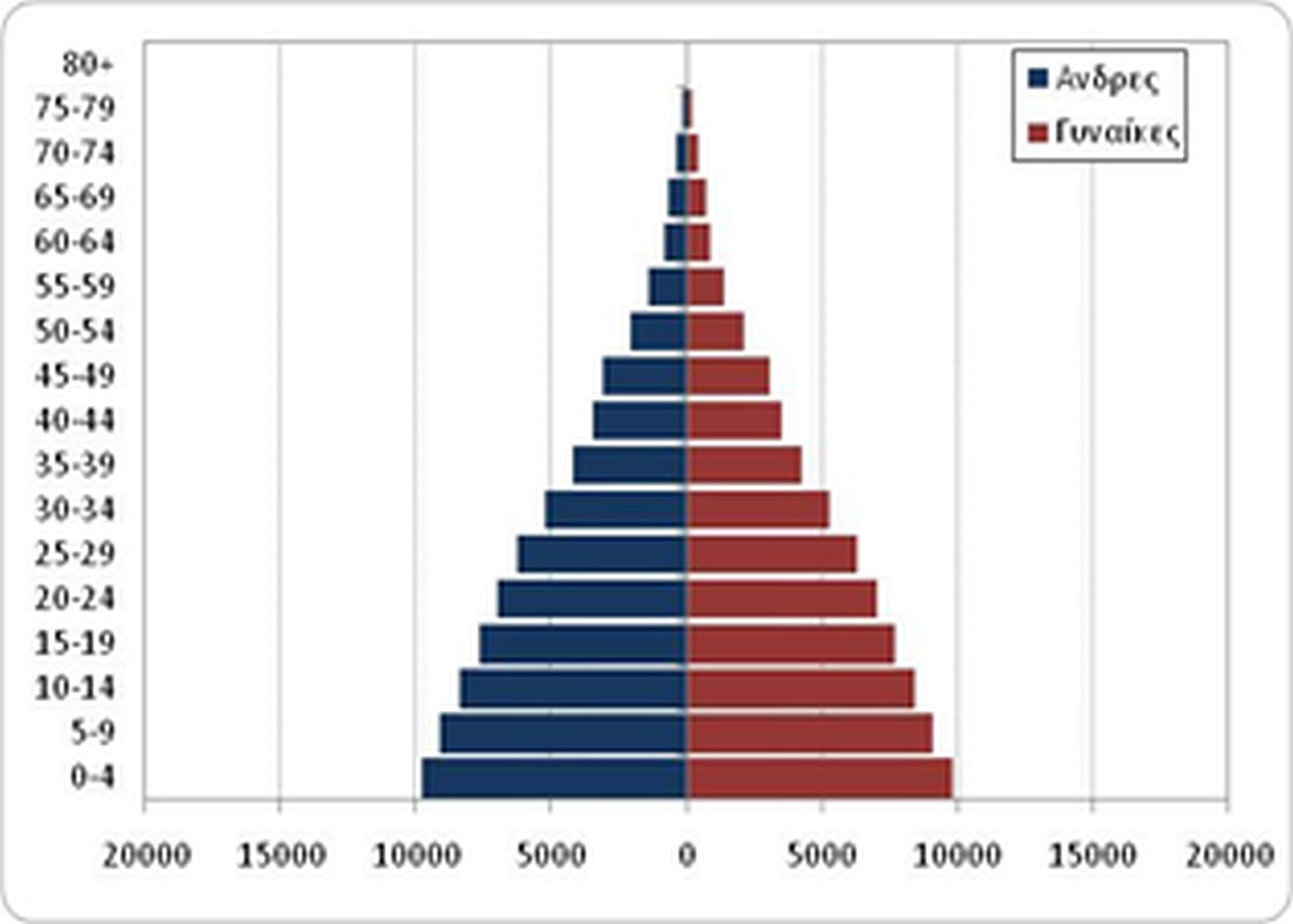
Τα παρακάτω διαγράμματα  (Διάγραμμα 5.5) αποδίδουν σε δύο διαφορετικές στιγμές -με μεταξύ τους απόσταση 100 ετών- τις πληθυσμιακές πυραμίδες διαφορετικών περιπτώσεων σταθερού πληθυσμού.

 

c. Στάσιμος πληθυσμός r= 0

Διάγραμμα 5.5 Πληθυσμιακές πυραμίδες σταθερού πληθυσμού, με r>0 (a), r<0 (b) r=0 (c)  δύο χρονικές στιγμές t και t+100.

 

5.4. Εκτιμήσεις και Προβολές του Πληθυσμού (Population Estimates and Projections)

Οι προοπτικές ανάπτυξης ενός πληθυσμού συνδέονται σε μεγάλο βαθμό με το σχεδιασμό των κοινωνικών και οικονομικών πολιτικών. Για το σχεδιασμό αυτό, απαραίτητες θεωρούνται οι πληροφορίες όχι μόνο για την τρέχουσα κατάσταση του πληθυσμού αλλά κυρίως για τις μελλοντικές προοπτικές του. Από το μέγεθος και τη σύνθεση του πληθυσμού καθορίζονται σε μεγάλο βαθμό οι δυνατότητες οικονομικής ανάπτυξης, οι κοινωνικές προτεραιότητες, οι μελλοντικές απαιτήσεις για υπηρεσίες, ενέργεια, τρόφιμα και νερό. Μια εικόνα του μελλοντικού πληθυσμού μιας συγκεκριμένης περιοχής είναι απαραίτητη για κάθε είδους προγραμματισμό και σχεδιασμό. Αυτή η εικόνα παρέχεται από τις πληθυσμιακές εκτιμήσεις και προβολές. Κυβερνητικοί παράγοντες, άτομα επιφορτισμένα με τη χάραξη πολιτικών, δημόσιοι φορείς, ερευνητές και ακαδημαϊκοί χρησιμοποιούν τις πληθυσμιακές προβολές αφ’ ενός για να σχεδιάσουν τις πολιτικές τους και αφ’ ετέρου για να εντοπίσουν έγκαιρα τις πιθανές συνέπειες θετικές ή αρνητικές των σύγχρονων τάσεων και των εν εξελίξει μεταρρυθμίσεων.

Σε αντίθεση με ορισμένα φυσικά φαινόμενα για τα οποία είναι δυνατή η ακριβής πρόγνωση ως προς το πού και πότε θα συμβούν, οι μακροπρόθεσμες δημογραφικές εξελίξεις είναι εξαιρετικά δύσκολο να προβλεφθούν με ακρίβεια. Ωστόσο, υπάρχουν κάποιες ιδιαιτερότητες των ανθρώπινων πληθυσμών οι οποίες διευκολύνουν την προσπάθεια πρόβλεψης. Η χαρακτηριστικότερη από αυτές είναι ο μεγάλος βαθμός επικάλυψης μεταξύ τρέχοντος και μελλοντικού πληθυσμού. Για παράδειγμα, ο πληθυσμός που σε δύο δεκαετίες θα είναι ηλικίας άνω των 20 ετών έχει ήδη γεννηθεί. Επιπλέον κάθε άτομο ενός πληθυσμού μεγαλώνει με την ίδια ταχύτητα: κατά ένα έτος κάθε χρόνο μέχρι τη στιγμή του θανάτου του. Συνεπώς, σ’ έναν κλειστό πληθυσμό, τη χρονική στιγμή t+1 στην ηλικία x+1 βρίσκονται όσα άτομα ήταν ηλικίας x τη χρονική στιγμή t, αφού αφαιρεθούν όσα άτομα απεβίωσαν στο διάστημα (t, t+1). Οι παραπάνω ειδικές συνθήκες περιορίζουν σημαντικά το εύρος των πληθυσμιακών μεταβολών και αποτελούν τη βάση για την ανάπτυξη σχετικών τεχνικών.

5.4.1. Πληθυσμιακές Εκτιμήσεις

Με τη βοήθεια των πληθυσμιακών εκτιμήσεων υπολογίζεται ο αριθμός των ατόμων που ζει σε μια περιοχή, μια συγκεκριμένη χρονική στιγμή (συνήθως την 1η Ιανουαρίου ή την 1η Ιουλίου κάθε έτους). Ο εκτιμώμενος πληθυσμός υπολογίζεται με την εφαρμογή διαφορετικών τεχνικών, ώστε να ποσοτικοποιηθεί η επίδραση των δημογραφικών γεγονότων στον πληθυσμό στο διάστημα που μεσολαβεί μεταξύ δύο απογραφών.

Οι διαφορετικές τεχνικές βασίζονται στην εφαρμογή κατάλληλων παραμετρικών υποδειγμάτων, όπως:

5.4.2.1 Απλό Γραμμικό Υπόδειγμα

Το απλό γραμμικό υπόδειγμα υποθέτει ότι ο πληθυσμός μεταξύ δύο χρονικών στιγμών ακολουθεί γραμμική αύξηση, δηλαδή ο ρυθμός μεταβολής είναι σταθερός. Με βάση αυτή την υπόθεση, ο πληθυσμός τη χρονική στιγμή t δίνεται από τη σχέση:

όπου P_o: το μέγεθος του πληθυσμού τη στιγμή της απογραφής
P_t: το εκτιμώμενο μέγεθος του πληθυσμού τη στιγμή t
r: ο σταθερός ρυθμός πληθυσμιακής αύξησης
t: το διάστημα σε έτη που μεσολαβεί μεταξύ των χρονικών στιγμών 0 και t

 

Η υπόθεση της γραμμικής εξέλιξης του πληθυσμού δεν είναι ρεαλιστική. Ωστόσο τα αποτελέσματα της μεθόδου θεωρούνται ικανοποιητικά για την εκτίμηση του πληθυσμού σε σύντομα χρονικά διαστήματα, όπως π.χ. για τα έτη που μεσολαβούν μεταξύ δύο απογραφών, με την προϋπόθεση ότι ο πληθυσμός δε βίωσε στο μεσοδιάστημα κάποια δραματική δημογραφική εμπειρία (π.χ. εμφύλιο πόλεμο, μη αναμενόμενα μεταναστευτικά ρεύματα, εφαρμογή πολιτικής μείωσης της γεννητικότητας, απότομη αύξηση των γεννήσεων).

5.4.2.2 Εκθετικό Υπόδειγμα
Δεδομένης της φύσης των δημογραφικών γεγονότων, η υπόθεση της εκθετικής αύξησης του πληθυσμού χρησιμοποιείται σε πολλές περιπτώσεις πληθυσμιακών εκτιμήσεων. Το μέγεθος του πληθυσμού τη χρονική στιγμή t δίνεται από τον τύπο:

όπου P_o: το μέγεθος του πληθυσμού τη στιγμή της απογραφής
P_t: το εκτιμώμενο μέγεθος του πληθυσμού τη στιγμή t
r: ο σταθερός ρυθμός πληθυσμιακής αύξησης
t: το διάστημα σε έτη το οποίο μεσολαβεί μεταξύ των χρονικών στιγμών 0 και t

 

5.4.2.3. Υπόδειγμα Λογιστικής Καμπύλης

Το υπόδειγμα της λογιστικής καμπύλης υποθέτει ότι η αύξηση του πληθυσμού, εκφρασμένη είτε ως ρυθμός (r) είτε ως απόλυτο μέγεθος δεν παραμένει διαχρονικά σταθερή. Αντίθετα, περιγράφει έναν πληθυσμό που αυξάνεται γρήγορα στην αρχή, στη συνέχεια όμως ο ρυθμός αύξησης r επιβραδύνεται, και προς το τέλος της περιόδου τείνει προς το μηδέν. Ο πληθυσμός δηλαδή προβλέπεται ότι δε θα ξεπεράσει ένα ανώτατο όριο.

όπου P_t: το εκτιμώμενο μέγεθος του πληθυσμού τη στιγμή t
Κ: το μέγιστο πληθυσμιακό μέγεθος κατά την εκτιμώμενη περίοδο
b: παράμετρος της οποίας η τιμή δηλώνει το χρονικό διάστημα μέχρι τη στιγμή που ο ρυθμός αύξησης θα αρχίσει να μειώνεται
α: ο μέσος ρυθμός πληθυσμιακής αύξησης της περιόδου
t: το συνολικό διάστημα σε έτη

5.4.2.4.Υπόδειγμα Πληθυσμιακών Συνιστωσών

Το υπόδειγμα πληθυσμιακών συνιστωσών βασίζει τον υπολογισμό του πληθυσμού μια χρονική στιγμή t στη θεμελιώδη δημογραφική εξίσωση. Έστω ότι είναι γνωστό με ακρίβεια το μέγεθος του πληθυσμού σε μια χρονική στιγμή 0. Ο υπολογισμός του πληθυσμού της στιγμή t προκύπτει από τη σχέση:

 

Η συγκεκριμένη σχέση, θα μπορούσε να εφαρμοστεί και ανάποδα, ώστε να υπολογιστεί το μέγεθος του πληθυσμού κάποια στιγμή του παρελθόντος για την οποία δεν υπάρχουν επίσημες στατιστικές.

Η συγκεκριμένη μέθοδος δίνει την καλύτερη εκτίμηση σε σχέση με τις προηγούμενες μεθόδους, όταν είναι γνωστά τα μεγέθη που αφορούν στα επί μέρους δημογραφικά γεγονότα. Αν και η πλήρης και αξιόπιστη καταγραφή των γεννήσεων και των θανάτων είναι γεγονός στις περισσότερο ανεπτυγμένες χώρες, η καταγραφή των μετακινήσεων δεν είναι στις περισσότερες περιπτώσεις πλήρης. Τα αποτελέσματα από την παραπάνω μέθοδο θα ήταν απολύτως ικανοποιητικά στη θεωρητική περίπτωση ενός κλειστού πληθυσμού.

5.4.2.5. Πληθυσμιακές Προβολές κατά Ηλικία και Φύλο

Πληθυσμιακή προβολή καλείται η υπολογιστική διαδικασία η οποία αποσκοπεί στην εκτίμηση του μεγέθους και της δομής του πληθυσμού σε μια μελλοντική χρονική στιγμή. Σε αντιδιαστολή με τις πληθυσμιακές εκτιμήσεις, οι προβολές δεν εκτιμούν μόνο το πληθυσμιακό μέγεθος αλλά και την κατά ηλικία και φύλο μελλοντική σύνθεση του πληθυσμού.

Για την κατάρτιση των πληθυσμιακών προβολών, χρησιμοποιείται ως αφετηρία μια χρονική στιγμή για την οποία υπάρχουν αναλυτικά στοιχεία ως προς τη δομή και σύνθεση του πληθυσμού, ενώ υιοθετούνται κάποιες συγκεκριμένες υποθέσεις σχετικά με την εξέλιξη των δημογραφικών συνιστωσών, της γονιμότητας, της θνησιμότητας και της μετανάστευσης. Δεδομένης της αβεβαιότητας ως προς την μελλοντική εξέλιξη αυτών των συνιστωσών, οι προβολές συνήθως υιοθετούν πέραν του βασικού (baseline) και κάποια εναλλακτικά σενάρια. Τα σχετικά με την εξέλιξη των πληθυσμιακών συνιστωσών σενάρια προκύπτουν από την παρατήρηση των τάσεων ή από τις εκτιμήσεις σχετικά με το ποιες θεωρείται πιθανό να παρατηρηθούν εντός του θεωρητικού πλαισίου.

Για την ανάπτυξη της μεθόδου απαιτούνται:

1. ο καθορισμός του έτους βάσης,
2. η διατύπωση του βασικού και των εναλλακτικών σεναρίων ως προς την κατά ηλικία εξέλιξη της γονιμότητας, της θνησιμότητας και των μετακινήσεων και τέλος
3. ο καθορισμός του χρονικού ορίζοντα της προβολής.

Έτος βάσης καλείται το έτος εκκίνησης της υπολογιστικής διαδικασίας για το οποίο πρέπει να είναι διαθέσιμη η αναλυτική κατά ηλικία και φύλο διάρθρωση του πληθυσμού. Η κατά ηλικία διάρθρωση του πληθυσμού μπορεί να παρουσιάζεται σε μονοετείς ή πενταετείς ηλικιακές ομάδες. Η εγκυρότητα των στοιχείων του έτους βάσης θεωρείται καθοριστική για την αξιοπιστία όλου του εγχειρήματος. Για το λόγο αυτό, ως βάση, χρησιμοποιούνται συνήθως τα πλέον πρόσφατα έτη των απογραφών.

Το βασικό σενάριο στηρίζεται, συνήθως, στην υπόθεση διατήρησης της τάσης των δεικτών γονιμότητας, θνησιμότητας και μετανάστευσης σε κάθε ηλικία. Τα εναλλακτικά σενάρια, προβλέπουν τη μελλοντική επιτάχυνση ή επιβράδυνση των τάσεων αυτών.

Ο ορίζοντας μιας πληθυσμιακής προβολής εξαρτάται από τον τρόπο αξιοποίησής της. Ωστόσο, είναι σαφές ότι όσο μεγαλώνει ο ορίζοντας τόσο αυξάνουν οι αποκλίσεις μεταξύ βασικού και εναλλακτικών σεναρίων και παράλληλα τόσο αυξάνεται η πιθανότητα σφάλματος.

• Η διαδικασία αποτελείται από επαναλαμβανόμενα βήματα, όπου το διάστημα της προβολής είναι ίσο με το εύρος των ηλικιακών ομάδων. Το μέγεθος μιας πληθυσμιακής ομάδας προκύπτει απ’ αυτό της αμέσως μικρότερης ηλικιακής ομάδας κατά την προηγούμενη χρονική στιγμή, αφού προηγουμένως εκτιμηθούν οι εκροές (θάνατοι και μεταναστευτική εκροή) και εισροές (μεταναστευτικές εισροές) από και προς αυτή.
• Όλες οι ηλικιακές ομάδες πρέπει να είναι του ιδίου εύρους. Μόνη εξαίρεση η τελευταία ομάδα η οποία είναι ανοικτή ως προς άνω άκρο της.
• Ο υπολογισμός του πληθυσμού κάθε πληθυσμιακής ομάδας γίνεται χωριστά.
• Κάθε χρονική στιγμή υπολογίζονται οι γεννήσεις καθώς και η πιθανότητα επιβίωσης των νεογέννητων, καθορίζοντας έτσι τον πληθυσμό της ηλικιακής ομάδας 0.

Τα βήματα επαναλαμβάνονται τόσες φορές όσα τα έτη που μεσολαβούν μεταξύ του έτους εκκίνησης και τελικού έτους της προβολής. Δεδομένου ότι κάθε επανάληψη στηρίζεται στα αποτελέσματα της προηγούμενης, όσο απομακρύνεται η διαδικασία από το έτος εκκίνησης τόσο μεγαλύτερο το ενδεχόμενο σφάλμα.

 

5.5. Βασικά στάδια της μεθοδολογίας

Σε κάθε ηλικιακή ομάδα επίσης επιδρά η μετανάστευση, είτε ως εκροή είτε ως εισροή ατόμων. Συνήθως, βάσει της προηγούμενης εμπειρίας προστίθεται ή αφαιρείται σε κάθε ηλικιακή ομάδα ένας αριθμός ατόμων.

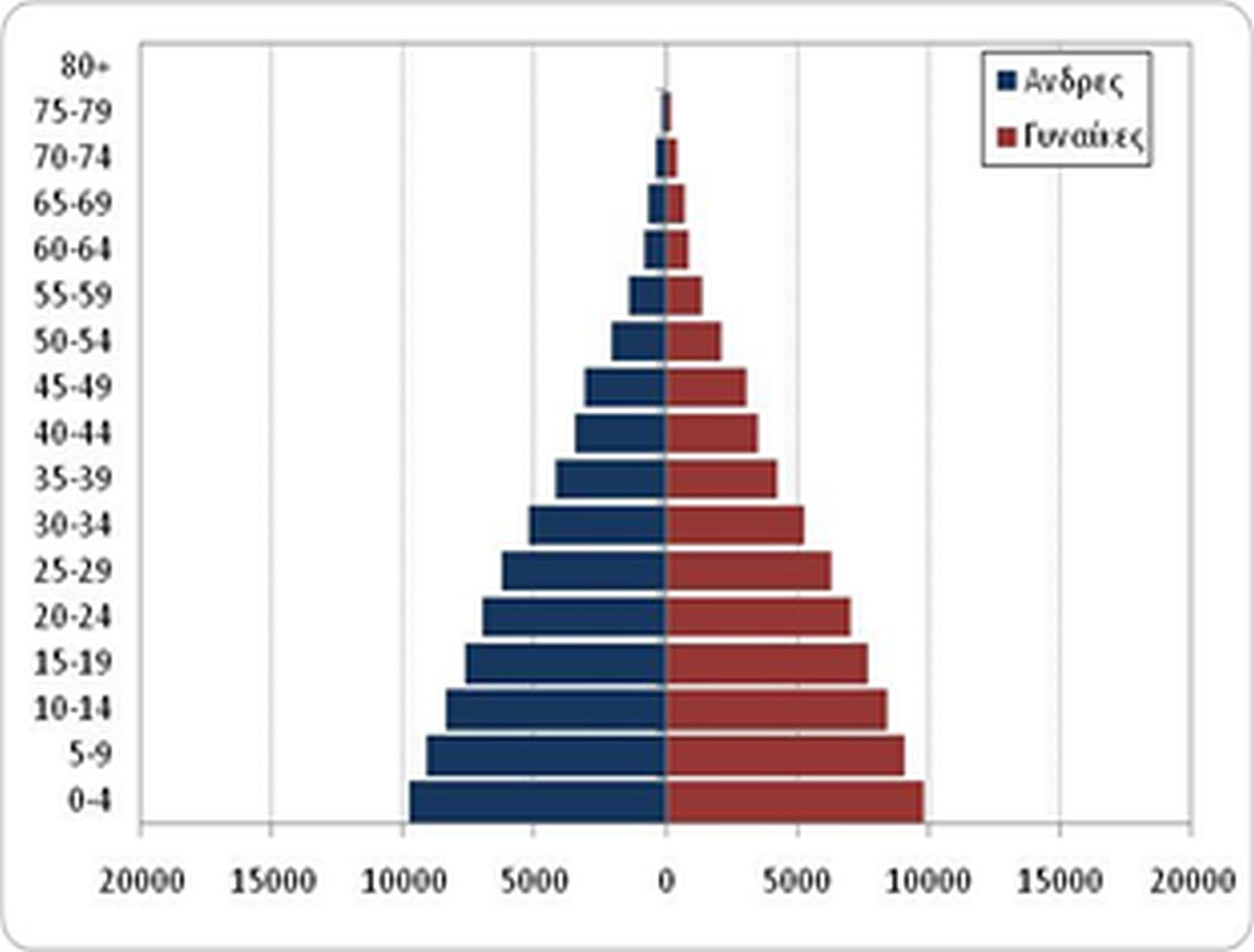
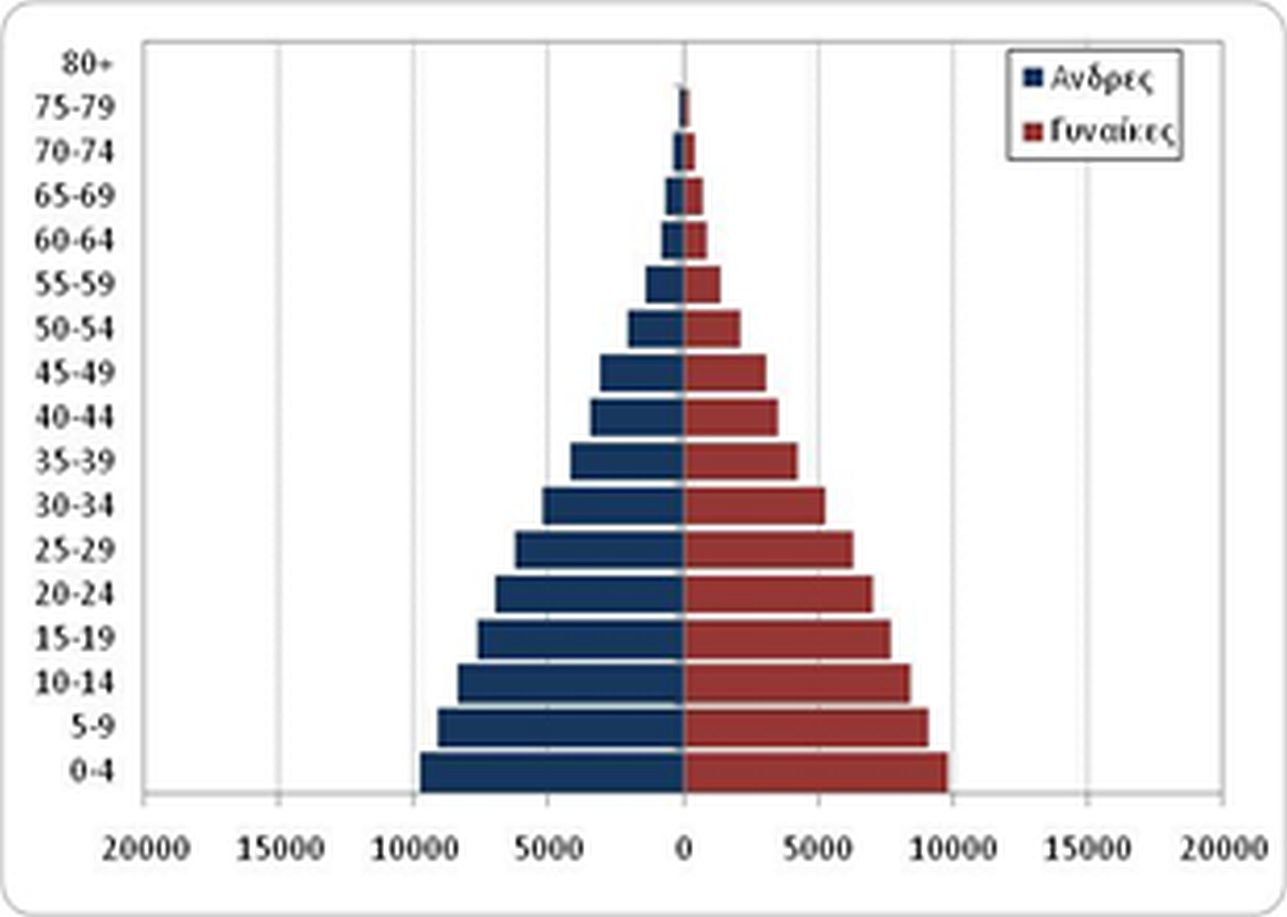
Παράδειγμα: Πληθυσμιακές προβολές του Γυναικείου πληθυσμού της Ελλάδας το 2016 με έτος εκκίνησης το 2011

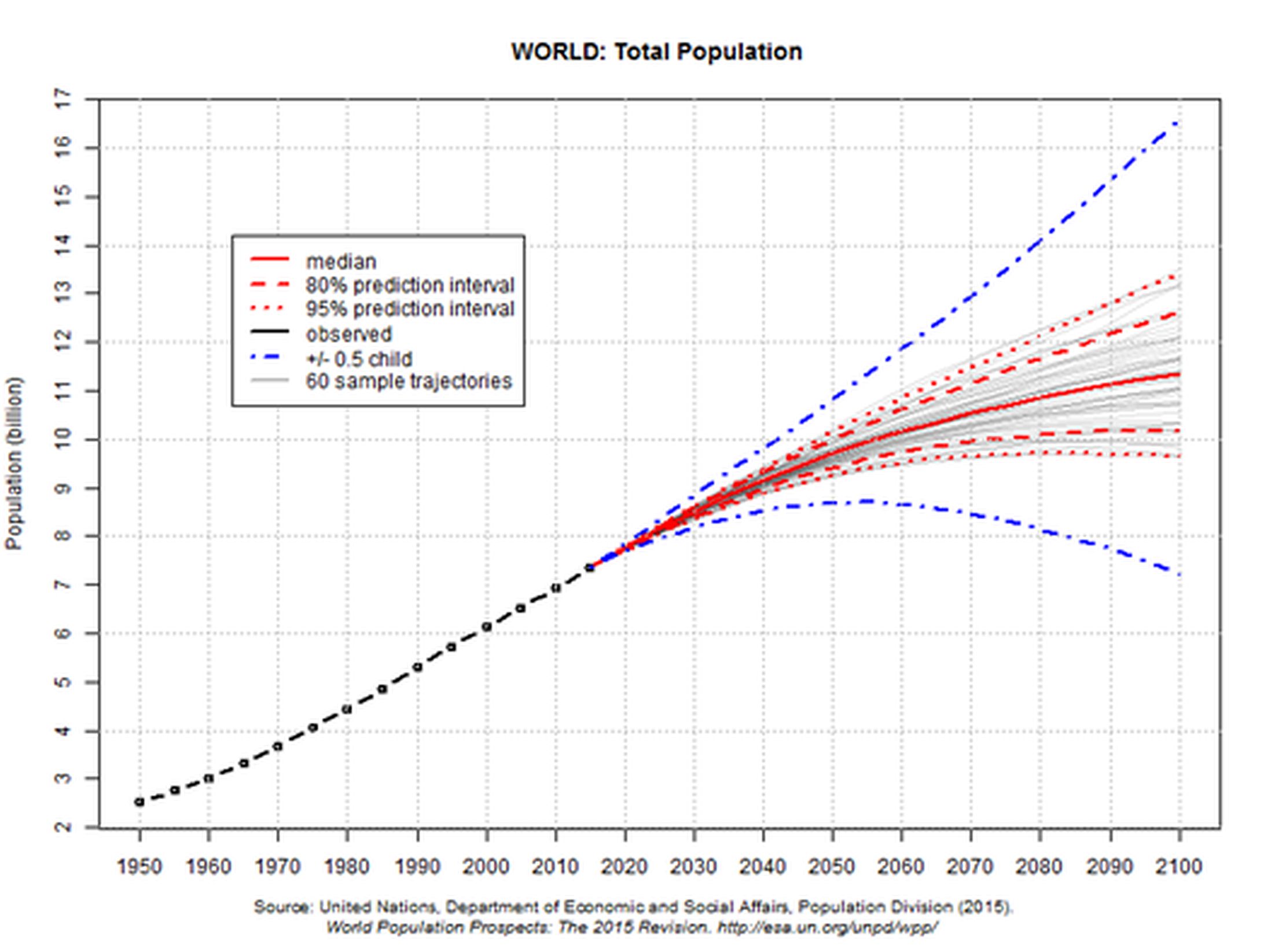
Στο Διάγραμμα 5.6 αποτυπώνεται το εύρος των εκτιμήσεων του μεγέθους του παγκόσμιου πληθυσμού έως το 2100, βάσει των προβολών του Ο.Η.Ε. (2015).

Διάγραμμα 5.6 Προβολές του παγκόσμιου Πληθυσμού έως το 2100, βασικό και εναλλακτικά σενάρια.

 

Οι πληθυσμιακές προβολές έχουν γενικά υψηλό βαθμό αξιοπιστίας, δεν αποτελούν, όμως, βεβαιότητες. Σύμφωνα με την Έκθεση της Εθνικής Ακαδημίας Επιστημών των Η.Π.Α. (National Academy of Sciences, NAS) η οποία αξιολογεί την προβλεπτική δύναμη των πληθυσμιακών προβολών, προκύπτει ότι η αξιοπιστία τους είναι συνάρτηση του διαστήματος προβολής και του γεωγραφικού επίπεδου ανάλυσης. Όσο πιο σύντομος ο χρονικός ορίζοντας της προβολής και όσο πιο συγκεντρωτικά τα αποτελέσματα (π.χ. λιγότερο ανεπτυγμένες περιοχές) τόσο μικρότερο το ενδεχόμενο σφάλμα (Bongaarts and Butalao, 2000).

Ακόμη και σε χώρες που έχει σημειωθεί ιδιαίτερη πρόοδος στη συλλογή και επεξεργασία των πληθυσμιακών στατιστικών, η ποιότητα ορισμένων δεδομένων (κυρίως σε σχέση με τις μεταναστευτικές ροές) παραμένει προβληματική θέτοντας σε αμφισβήτηση το αποτέλεσμα των προβολών. Συχνά, ορισμένα φαινόμενα τα οποία θα ήταν χρήσιμο να προβλεφθούν με τη μεγαλύτερη δυνατή ακρίβεια, είναι εκείνα για τα οποία τα στοιχεία είναι ελλιπή και προκύπτουν οι λιγότερο αξιόπιστες εκτιμήσεις (πχ μετακινήσεις εσωτερικές και διεθνείς). Μια επιπλέον δυσκολία στην κατάρτιση αξιόπιστων προβολών είναι η σωστή εκτίμηση των μελλοντικών τάσεων των δημογραφικών γεγονότων. Εμπειρικά έχει αποδειχθεί ότι η εξέλιξη της γονιμότητας είναι περισσότερο αβέβαιη σε σχέση με αυτήν της θνησιμότητας. Η υπο-εκτίμηση της ταχύτητας μείωσης της γονιμότητας αποτέλεσε την κύρια πηγή αποκλίσεων μεταξύ προβολών και πραγματικών τάσεων κατά τα τελευταία 20 χρόνια. Ένας ακόμη παράγοντας ο οποίος υπεισέρχεται προκαλώντας αποκλίσεις μεταξύ προβολών και πραγματικότητας είναι το απρόβλεπτο. Κανένας δημογράφος δε θα μπορούσε να προβλέψει τη δραματική επίπτωση του AIDS στη θνησιμότητα των χωρών της υπο-Σαχάριας Αφρικής κατά την τελευταία δεκαετία του προηγούμενου αιώνα.

Ωστόσο, και παρά τις όποιες αδυναμίες, τα αποτελέσματα των πληθυσμιακών προβολών παρουσιάζουν μεγαλύτερο βαθμό ακρίβειας από άλλες εκτιμήσεις (όπως πχ τιμή του πετρελαίου).

Άλλωστε, αποτελούν ένα από τα ελάχιστα εργαλεία χαρτογράφησης και σχεδιασμού του μέλλοντος.

 

Βιβλιογραφικές Αναφορές

• Bongaarts, J. & R. Bulatao, (eds) (2000) Beyond Six Billion: Forecasting the World’s Population, Committee on PopulationCommission on Behavioral and Social Sciences and Education, National Research Council, Washington, DC.
• Coale, A. and J. Trussell (1996) “The Development and Use of Demographic Models”, Population Studies, 50 Q3, 469-484.
• Hinde, A. (1998) Demographic Methods, London: Arnold Publishers
• Preston, S., Heuveline, P. & M. Guillot (2001). Demography: measuring and modeling population processes, Blackwell Publishers.
• United Nations (2015) World Population Prospects, The 2015 Revision, Population Division Department of Economic and Social Affairs, New York.
• Weinstein, J. and V.Pillai (2001) Demography: the science of population, Allyn and Bacon.
  
  
  
• Παπαδάκης Μ, Κ. Τσίμπος (2004) Δημογραφική Ανάλυση, Αρχές-Μέθοδοι-Υποδείγματα, Εκδόσεις Σταμούλης, Αθήνα.
• Σιάμπος, Γ. (1993) Δημογραφία, Εκδόσεις Κ.Π. Σμπίλιας, Αθήνα.